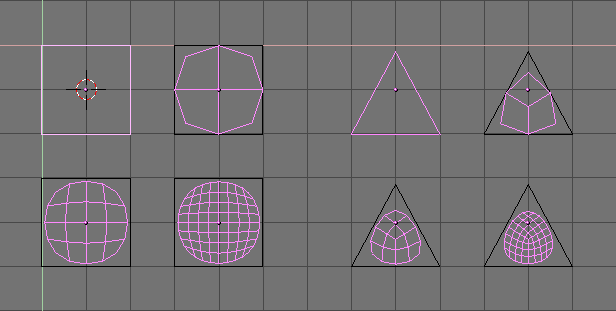Catmull-Clark Subdivision Surfaces
Catmull-Clark Subdivision Surfaces or, in short SubSurf, is a mathematical algorithm to compute a "smooth" subdivision of a mesh. With any regular Mesh as a starting point, Blender can calculate a smooth subdivision on the fly; while modelling or while rendering. This allows high resolution Mesh modelling without the need to save and maintain huge amounts of data. This also allows for a smooth 'organic' look to the models.
Actually a SubSurfed Mesh and a NURBS surface have many points in common inasmuch as both rely on a "coarse" low-poly "mesh" to define a smooth "high definition" surface, but there are also notable differences:
NURBS have finer control on the surface, since you can set "weights" independently on each control point of the control mesh. On a SubSurfed mesh you cannot act on weights.
SubSurfs have a more flexible modelling approach. Since a SubSurf is a mathematical operation occurring on a mesh, you can use all the modelling techniques described in this Chapter on the mesh, which are more numerous, and far more flexible, than those available for NURBS control polygons.
SubSurf is a Mesh option, the button to activate this is in the EditButtons F9 (Figure 55). The NumButtons immediately below it define, on the left, the resolution (or level) of subdivision for 3D visualization purposes, the one on the right the resolution for rendering purposes.
Since SubSurf computations are performed both real-time, while you model, and at render time, and they are CPU intensive, it is usually good practice to keep the SubSurf level low (but non-zero) while modelling and higher for rendering.
Figure 56 and Figure 57 shows, respectively, a rendering of a SubSurf mesh and the original, un-SubSurfed mesh.
Figure 58 shows a 0,1,2,3 level of SubSurf on a single square face or on a single triangular face. Such a subdivision is performed, on a generic mesh, for each square or rectangular face.
It is evident how each single quadrilateral face produces 4^n faces in the SubSurfed mesh, n being the SubSurf level, or resolution, while each triangular face produces 3*4^(n-1) new faces (Figure 58). This dramatic increase of face (and vertex) number reflects in a slow-down of all editing, and rendering, actions and calls for lower SubSurf level in the Editing process than in the rendering one.
Blender's subdivision system is based on the Catmull-Clarke algorithm. This produces nice smooth SubSurf meshes but any 'SubSurfed' face, that is, any small face created by the algorithm from a single face of the original mesh, shares the normal orientation of that original face.
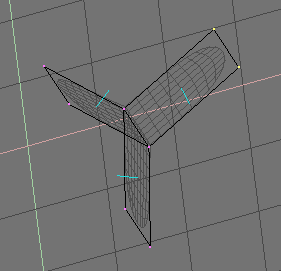
This is not an issue for the shape itself, as Figure 59 shows, but it is an issue in the rendering phase, and in solid mode, where abrupt normal changes can produce ugly black lines (Figure 60).
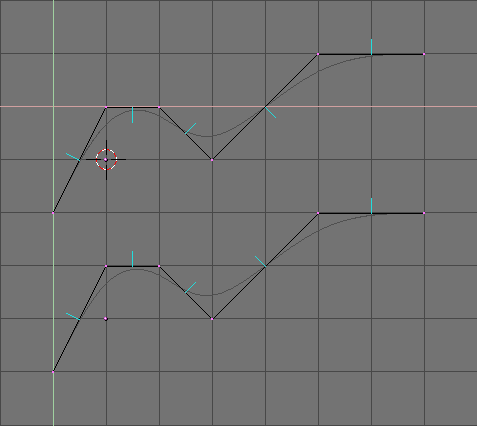
Figure 59. Side view of subsurfed meshes. With random normals (top) and with coherent normals (bottom)
Use the CTRL+N command in EditMode and with all vertices selected to make Blender recalculate the normals.
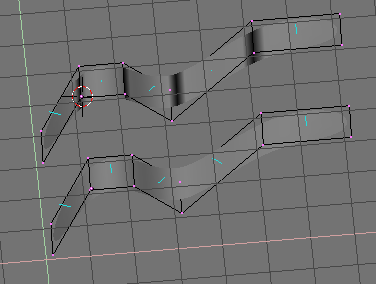
Figure 60. Solid view of SubSurfed meshes with inconsistent normals (top) and consistent normals (bottom).
In the images the face normals are drawn cyan. You can enable drawing normals in the EditButtons (F9) menu.
It is worth noting that Blender cannot recalculate normals correcty if the mesh is not "Manifold". A "Non-Manifold" mesh is a mesh for which an 'out' cannot unequivocally be computed. Basically, from the Blender point of view, it is a mesh where there are edges belonging to more than two faces.
Figure 61 shows a very simple example of a "Non-Manifold" mesh. In general a "Non-Manifold" mesh occurs when you have internal faces and the like.
A "Non-Manifold" mesh is not a problem for conventional meshes, but can give rise to ugly artifacts in SubSurfed meshes, and does not allow decimation, so it is better to avoid them as much as possible.
You can tell that a mesh is "Non Manifold" from two hints:
The Recalculation of normals leaves black lines somewhere
The "Decimator" tool in the EditButtons refuses to work stating that the mesh is "No Manifold"
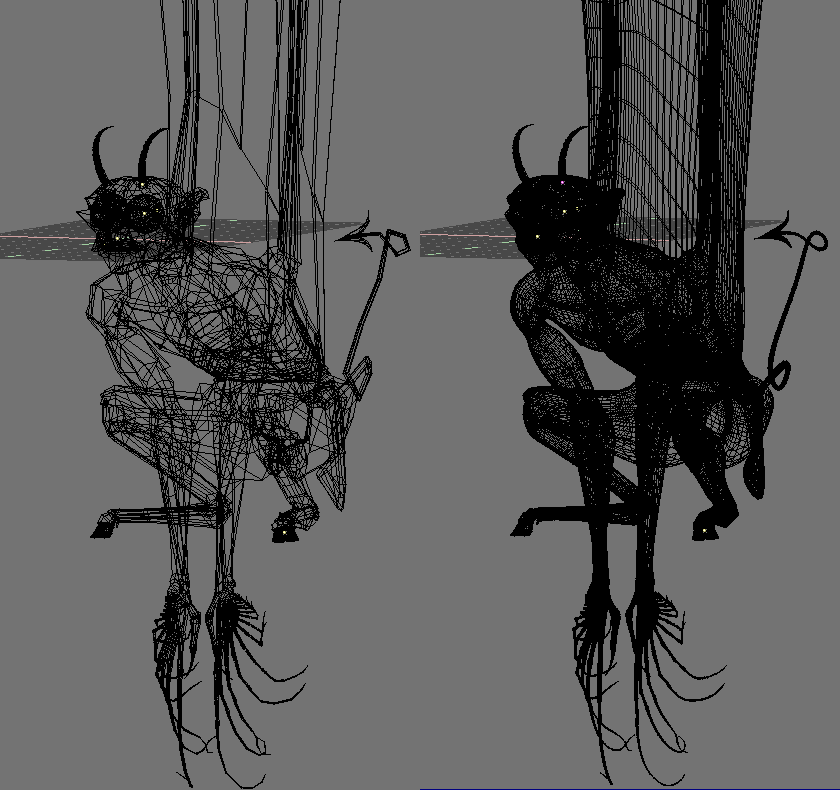
The SubSurf tool allows for very good "organic" models, but keep in mind that a regular Mesh with square faces gives the best result.
Figure 62 and Figure 63 shows an example of what can be done with Blender SubSurfs.